因子分析
因子分析(Factor Analysis,FA)
用少数几个假象变量来表示其根本的数据结构,能反应原来众多变量的主要信息。因子分析的前提条件是观测变量间有较强的相关性,这样才能有共享因子。
步骤
- 选择分析变量
- 计算所选原始变量的相关系数矩阵
- 提取公共因子,确定因子数目
- 因子旋转,解释因子
- 计算因子得分
模型
本文的变量名大体可分为三种:大写粗体、大写、小写。
大写粗体一般表示整个矩阵,一般为二维;大写参数一般表示为指标/因子,包含 \(n\) 个元素(观测值)可以看作向量;小写表示元素或单个变量。
数学模型
记 \(m\) 个观测值 \(X_i(i=1,2,\dots,m)\) 可以表示为
\[X_{i}=\mu_{i}+\alpha_{i 1} F_{1}+\cdots+\alpha_{i m} F_{m}+\varepsilon_{i}\]
即 \[\left[\begin{array}{c} X_{1} \\ X_{2} \\ \vdots \\ X_{m} \end{array}\right]=\left[\begin{array}{c} \mu_{1} \\ \mu_{2} \\ \vdots \\ \mu_{m} \end{array}\right]+\left[\begin{array}{cccc} \alpha_{11} & \alpha_{12} & \cdots & \alpha_{1 r} \\ \alpha_{21} & \alpha_{22} & \cdots & \alpha_{2 r} \\ \vdots & \vdots & & \vdots \\ \alpha_{m 1} & \alpha_{m 2} & \cdots & \alpha_{m r} \end{array}\right]\left[\begin{array}{c} F_{1} \\ F_{2} \\ \vdots \\ F_{r} \end{array}\right]+\left[\begin{array}{c} \varepsilon_{1} \\ \varepsilon_{2} \\ \vdots\\ \varepsilon_{m} \end{array}\right]\] 即 \[\boldsymbol{X}-\boldsymbol{\mu}=\boldsymbol{\Lambda}\boldsymbol{F}+\boldsymbol{\varepsilon}\]
满足:
- \(E(\boldsymbol{F})=0\) 且 \(E(\boldsymbol{\varepsilon})=0\)
- 载荷因子 \(F_i\) 之间无线性关系: \(Cov(\boldsymbol{F})=E_m\)
- 特殊因子 \(\varepsilon_i\) 之间无线性关系: \(Cov(\boldsymbol{\varepsilon})=D(\boldsymbol{\varepsilon})=diag(\sigma _1^2,\sigma _2^2,\dots,\sigma _m^2)\)
- 特殊因子和载荷因子无线性关系:\(Cov(\boldsymbol{F},\boldsymbol{\varepsilon})=0\)
模型的性质
- 原子变量 \(\boldsymbol{X}\) 的协方差矩阵分解
由 \(\boldsymbol{X}-\boldsymbol{\mu}=\boldsymbol{\Lambda}\boldsymbol{F}+\boldsymbol{\varepsilon}\) 得 \(Cov(\boldsymbol{X}-\boldsymbol{\mu})=\boldsymbol{\Lambda}Cov(\boldsymbol{F})\boldsymbol{\Lambda}^T+Cov(\boldsymbol{\varepsilon})\) 即
\[Cov(\boldsymbol{X})=\boldsymbol{\Lambda}\boldsymbol{\Lambda}^T+D(\boldsymbol{\Lambda})\]
\(\sigma _1^2,\sigma _2^2,\dots,\sigma _m^2\) 的值越小,公共因子贡献成分越多。
- 因子载荷矩阵不唯一(可旋转的原因)
设 \(\Gamma\) 是一个标准正交矩阵,有 \[\widetilde{\boldsymbol{\Lambda}}=\boldsymbol{\Lambda}\Gamma , \widetilde{\boldsymbol{F}}=\Gamma^{\tiny T}\boldsymbol{F} \] \[\boldsymbol{X}=\boldsymbol{\mu}+\widetilde{\boldsymbol{\Lambda}}\widetilde{\boldsymbol{F}}+\boldsymbol{\varepsilon}\]
载荷矩阵统计性质
- \(\alpha_{i j}\) 的含义
因子载荷矩阵 \(\alpha_{i j}\) 表示第 \(i\) 个变量与第 \(j\) 个公共因子的相关系数,反应第 \(i\) 个变量与第 \(j\) 个公共因子的相关重要性。 \(|\alpha_{i j}|\) 越大,相关的密切程度越高。
- 变量共同度的统计意义
变量 \(X_i\) 的共同度是因子载荷矩阵第 \(i\) 行的元素平方和,记 \(h_i^2=\sum\limits_{j=1}^{r}\alpha_{ij}^2\)
因为
\[Var(X_i)=\alpha_{i1}^2Var(F_1)+\dots+\alpha_{ir}^2Var(F_r)+Var(\varepsilon_i)\]
得
\[1=\sum\limits_{j=1}^{r}\alpha_{ij}^2+\sigma_i^2\]
可以看出 \(h_i^2\) 越靠近 \(1\) , \(\sigma_i^2\) 越靠近 \(0\) , 原变量 \(X_i\) 被公共因子表现的越好。
- 公共因子 \(F_j\) 的方差贡献统计意义
因子 \(F_j\) 的方差贡献和是因子载荷矩阵第 \(j\) 列的平方和,记为 \(S_j=\sum\limits_{i=1}^{m} \alpha_{ij}^2=\lambda_j\)
用于衡量 \(F_j\) 的相对重要性。
- 残差阵
用原协方差阵减去公因子协方差阵与特殊因子协方差阵,得到残差阵
\[(\epsilon_{ij})_{m\times m} = \boldsymbol{R}-(\boldsymbol{\Lambda}\boldsymbol{\Lambda}^T+\boldsymbol{D})\]
残差阵元素的平方和为残差平方和
\[Q(m)=\sum\limits_{i=1}^{m}\sum\limits_{j=1}^{m}\epsilon_{ij}^2 \le \sum\limits_{k=r+1}^{m}\lambda_k^2\]
因子载荷矩阵估计法
主成分分析法
和“主成分分析”本质相同,主成分分析是将样本经过载荷矩阵 \(\boldsymbol{P}\) 变换到坐标轴上使得坐标轴方向方差最大;因子分析的主成分分析法相当于主成分分析的逆过程,因子代表的 \(\R^r\) 空间上的点,经过因子载荷矩阵 \(\boldsymbol{\Lambda}\) 变换后得原样本点。
设样本相关系数矩阵为 \(\boldsymbol{R}\) ,计算其特征值为 \(\lambda_1,\lambda_2,\dots,\lambda_m\) (\(\lambda_1\ge \lambda_2\ge \dots\ge \lambda_m\)) ,对应的特征向量为 \(\boldsymbol{\eta} _1,\boldsymbol{\eta} _2,\dots,\boldsymbol{\eta} _m\) ,记 \(\boldsymbol{H}=[\boldsymbol{\eta }_1,\boldsymbol{\eta }_2,\dots,\boldsymbol{\eta }_m]\) 有
\[\boldsymbol{R}=\boldsymbol{H}\begin{bmatrix} \boldsymbol{\lambda_1}& & & \\ & \boldsymbol{\lambda_2} & & \\ & &\ddots & \\ & & & \boldsymbol{\lambda_1} \end{bmatrix}\boldsymbol{H}^T=\boldsymbol{\Lambda}\boldsymbol{\Lambda}^T+D\]
( \(\small\boldsymbol{D}\) 被忽略)即因子载荷矩阵为
\[\boldsymbol{\Lambda}=[\sqrt{\lambda_1}\boldsymbol{\eta_1},\sqrt{\lambda_2}\boldsymbol{\eta_2},\dots,\sqrt{\lambda_m}\boldsymbol{\eta_m}]\]
使得公共因子方差贡献\(S_j=\lambda_j\)
根据碎石图,用碎石原则确定因子个数 \(r\)。
特殊因子方差可以用 \(\boldsymbol{R}-\boldsymbol{\Lambda}\boldsymbol{\Lambda}^T\) 的主对角线元素估计: \[\sigma_i^2=1-\sum_{j=1}^m\alpha_{ij}^2\]
缺点:上式有一个假定,模型中的特殊因子是不重要的,因而从 \(\boldsymbol{R}\) 的分解中忽略了特殊因子的方差。所得的特殊因子 \(\varepsilon_{1},\varepsilon_{2},...,\varepsilon_{p}\) 之间并不相互独立,不完全符合假设前提。因此,当共同度较大时,特殊因子所起作用小时,它们之间存在的相关性所带来的影响可以几乎忽略。实际应用中,可以先用主成分法进行分析,再尝试其他方法。
主因子法
主因子方法是对主成分方法的修正,假定我们首先对变量进行标准化变换。则
\[\boldsymbol{R}=\boldsymbol{\Lambda}\boldsymbol{\Lambda}^T+\boldsymbol{D}\\ \boldsymbol{R}^*=\boldsymbol{\Lambda}\boldsymbol{\Lambda}^T=\boldsymbol{R}-\boldsymbol{D}\]
式中 \(\boldsymbol{R}^*\) 为约相关系数矩阵,其对角线上的元素为 \(h_i^2\) 。
特殊因子方差是未知的,一般通过样本估计得到。方法可以有;
- 取 \(\hat{h_i^2}=1\) ,这种情况下主因子解与主成分分解等价
- 取 \(\hat{h_i^2}=\max\limits_{\tiny i \ne j}|r_{ij}|\) ,取 \(X_i\) 与其他指标简单相关系数最大者
- 取 \(\hat{h_i^2}=\frac{1}{m-1}\sum\limits_{sj=1,j\ne i}^{m}r_{ij}\) ,其中要求该值为正数
记
\[\boldsymbol{R}^*=\boldsymbol{R}-\boldsymbol{D}=\left[\begin{array}{cccc} \hat{h_{1}^{2}} & r_{12} & \cdots & r_{1 m} \\ r_{21} & \hat{h_{2}^{2}} & \cdots & r_{2 m} \\ \vdots & \vdots & & \vdots \\ r_{m 1} & r_{m 2} & \cdots & \hat{h_{m}^{2}} \end{array}\right]\]
直接求出 \(\boldsymbol{R}^*\) 的特征值为 \(\lambda_1^*,\lambda_2^*,\dots,\lambda_m^*\) (\(\lambda_1^*\ge \lambda_2^*\ge \dots\ge \lambda_m^*\)) ,和对应的特征向量为 \(\boldsymbol{\eta} _1^*,\boldsymbol{\eta} _2^*,\dots,\boldsymbol{\eta} _m^*\) ,得到载荷矩阵:
\[\boldsymbol{\Lambda}=[\sqrt{\lambda_1^*}\boldsymbol{\eta}_1^*,\sqrt{\lambda_2^*}\boldsymbol{\eta}_2^*,\dots,\sqrt{\lambda_m^*}\boldsymbol{\eta}_m^*]\]
极大似然估计法
假设数据 \(X_1,...,X_n\) 服从 \(m\) 元正态,公因子与特殊因子也假定服从正态。
\[L(\mu, \boldsymbol{\Lambda}, \boldsymbol{D})=\prod_{i=1}^{d} \frac{1}{(2 \pi)^{m / 2}|\boldsymbol{R}|^{1 / 2}} \exp \left[-\frac{1}{2}\left(\boldsymbol{X}_{\mathbf{i}}-\mu\right)^{\prime} \boldsymbol{\boldsymbol{R}}^{-1}\left(\boldsymbol{X}_{\mathbf{i}}-\mu\right)\right]\]
用数值极大化的方法可以得到极大似然估计。
Matlab 工具箱求因子载荷矩阵使用的是最大似然估计,其命令为
factoran 。
因子旋转
建立因子模型不仅要得到公共因子,还要能解释这些公共因子的具体含义。
由于因子载荷矩阵不唯一,所以可以对载荷矩阵进行旋转,使得载荷矩阵每行或每列的元素平方值向 \(0\) 和 \(1\) 两极分化,即使信息分布尽可能不均匀,也就是信息要集中分布于几个不同的因子上。
\[\boldsymbol{X} = \boldsymbol{\Lambda }\Gamma {\Gamma ^{ - 1}} \boldsymbol{F} + \boldsymbol{\varepsilon}\]
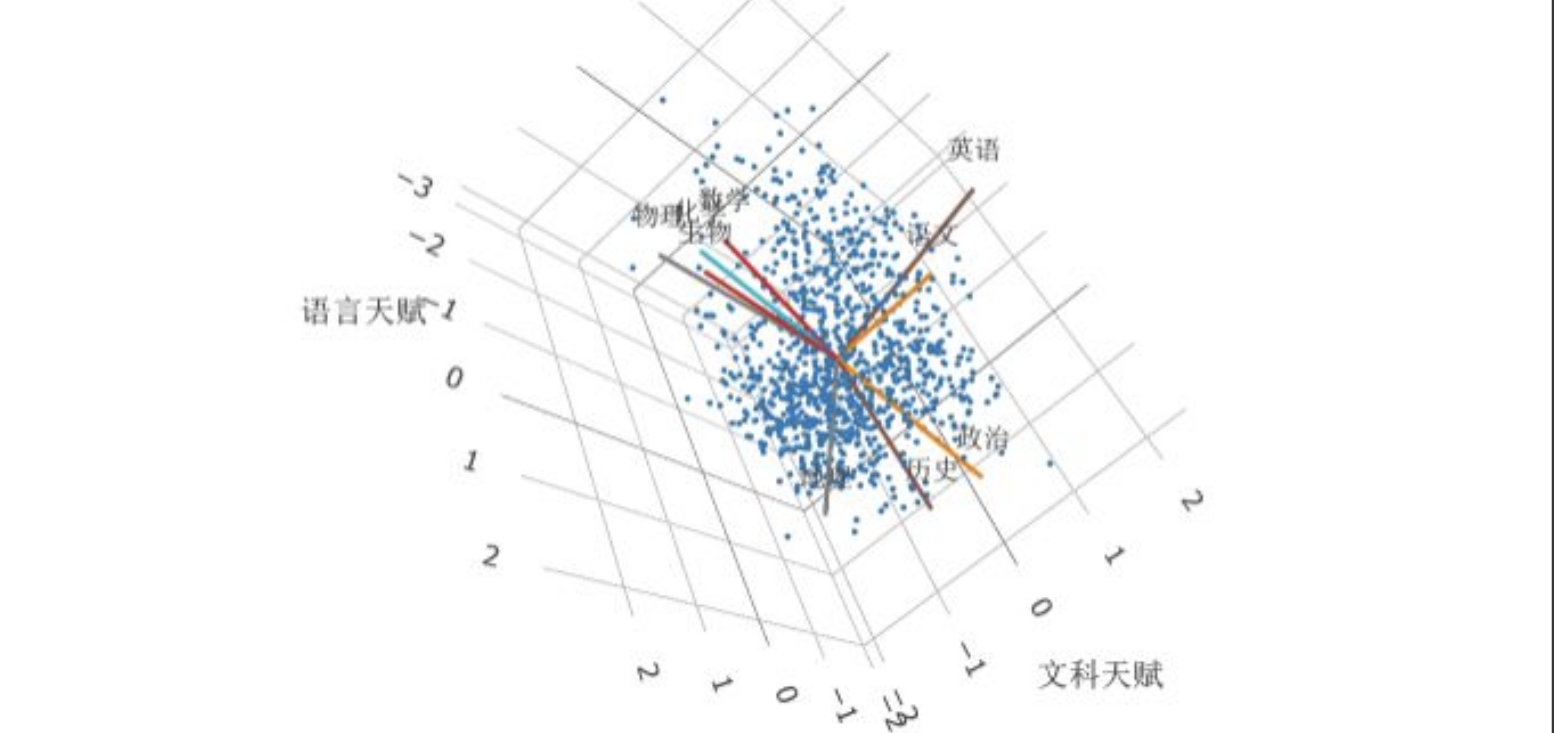
因为是对整个 \(\R^r\) 的空间正交变换(可以理解为坐标轴旋转或者样本旋转),所以银子旋转不会是损耗信息量只会改变因子载荷矩阵的权重分配,变量共同度 \(h_i^2\) 不变,因子方差贡献 \(S_j\) 不变(正交旋转不改变向量长度)。
对于任意两列,正交矩阵形式可以设为
\[\Gamma=\left[\begin{array}{ll} \cos \phi & -\sin \phi \\ \sin \phi & \cos \phi \end{array}\right]\\\]
带入得到
\[\boldsymbol{\Lambda}^*=\boldsymbol{\Lambda} \Gamma=\left[\begin{array}{ll} \alpha_{11} \cos \phi+\alpha_{12} \sin \phi & -\alpha_{11} \sin \phi+\alpha_{12} \cos \phi \\ \vdots & \vdots \\ \alpha_{p 1} \cos \phi+a_{p 2} \sin \phi & -\alpha_{p 1} \sin \phi+\alpha_{p 2} \cos \phi \end{array}\right]= \left[\begin{array}{ll} \alpha_{11}^* & \alpha_{12}^*\\ \vdots & \vdots \\ \alpha_{m 1}^* &\alpha_{m2}^* \end{array}\right]\]
方差最大的正交旋转
基本思想: \(\alpha_{ij}^*\) 表示变量 \(i\) 与因子 \(j\) 的关联程度,要使每一列的元素值越分散,就要 使因子载荷矩阵的每一列元素的方差更大。
因为 \(r<m\) ,每一行向量的长度不统一,所以先对每一行都除以共同度 \(h_i^2\) ,记
\[d_{i j}=\frac{ { \alpha_{i j}^{*} }^2 }{h_i^2} , \scriptsize (i=1,2,\dots,m,j=1,2,\dots,r)\]
定义因子载荷第 j 列的方差为
\[V_{j}=\frac{1}{m}\sum\limits_{\tiny i=1}^{\tiny m}\left(d_{i j}^{2}-\bar{d}_{j}\right)^{2}=\frac{1}{m^2}\left[m \sum_{i=1}^{m} d_{ij}^2-{\left(\sum_{i=1}^{m} d_{ij}\right)}^{2}\right]\\\]
其中 \(\bar{d}_{j}=\frac{1}{m} \sum\limits_{\tiny i=1}^{\tiny m} d_{i j}^{2}\)
定义因子载荷矩阵 \(\boldsymbol{\Lambda}\) 的方差等于每一列的方差之和
\[V=\sum_{j=1}^rV_{j}=\frac{1}{m^2}\sum_{j=1}^{r}\left[m \sum_{i=1}^{m} d_{ij}^2-{\left(\sum_{i=1}^{m} d_{ij}\right)}^{2}\right]\]
- 二维空间
设因子载荷矩阵有两列 \(r=2\) ,
\[\boldsymbol{\Lambda}^*=\boldsymbol{\Lambda} \Gamma=\left[\begin{array}{ll} \alpha_{11}^* & \alpha_{12}^*\\ \vdots & \vdots \\ \alpha_{m 1}^* &\alpha_{m2}^* \end{array}\right]\\\]
将 \(\boldsymbol{\Lambda}^*\) 带入 \(V_{\boldsymbol{\Lambda}}\) ,让 \(V_{\boldsymbol{\Lambda}^*}\) 对 \(\phi\) 求导数
令
\[\frac{\partial V_{\boldsymbol{\Lambda}}}{\partial \phi}=0\]
得到 \(\phi\) 应该满足
\[\tan 4 \phi=\frac{d-2 ab / m}{c-\left(a^{2}-b^{2}\right) / m}\]
其中,若记
\[\mu_{i}=d_{i1}-d_{i2} , \quad \nu_{i}=2 \frac{\alpha_{i 1}\alpha_{i 2}}{h_{i}^{2}}=2\sqrt{d_{i1}d_{i2}}\]
则
\[ \begin{array}{c} a=\sum\limits_{i=1}^{m} \mu_{i}, \quad b=\sum\limits_{i=1}^{m} \nu_{i}, \\ c=\sum\limits_{i=1}^{m}\left(\mu_{i}^{2}-\nu_{i}^{2}\right), \quad d=2 \sum\limits_{i=1}^{m} \mu_{i} \nu_{i} . \end{array} \]
- 高维空间
当 \(m{\small>}2\) 时, 可逐次对每两个因子 \(F_{i}, F_{j}\small (i \neq j)\) 进行以上旋转。
选择正交旋转的角度 \(\varphi_{i j}\) ,即使这两个因子的方差之和达最大。 \(m\) 个因子的全部配对旋转, 共需旋转 \(C_{m}^{2}\) 次,全部旋转 完毕即算一次循环 (或一轮)。经第一轮旋转后计算所得的因子载荷 方差 \(V_{(1)}\) , 此时不能认为 \(V_{(1)}\) 就是最大方差,还需从旋转后的载荷矩 阵出发, 再进行第二轮、第三轮旋转, 直到 \(V\) 不能再增大为止[5]。
四次方最大化旋转
基本思想: 使得因子载荷的每一行只在少部分地方取较大的值,每个变量只在一个因子上有较高的载荷,即 使因子载荷矩阵每一行的元素方差最大化。
用于度量方差的量为
\[Q=\sum_{i=1}^{m} \sum_{j=1}^{r}\left({\alpha_{i j}^{*}}^2-\frac{1}{r}\right)^{2} \overset{\tiny 化}{=} \sum_{i=1}^{m} \sum_{j=1}^{r}\left({\alpha_{i j}^{*}}^4-2+\frac{m}{r}\right)\]
得到最简式
\[Q=\sum_{i=1}^{m} \sum_{j=1}^{r}{\alpha_{i j}^{*}}^4\]
这里的 \(1/r\) 可以理解为近似的每一行均值。
等量最大法
基本思想: 同时考虑载荷矩阵每行的方差和每列的方差,对其加权平均最大化。
\(V\) 近似化简为 \[V=-\frac{1}{m}\sum_{j=1}^{r}{\left(\sum_{i=1}^{m} d_{ij}\right)}^{2}\quad\color{Gray} \tiny ,\sum_{i=1}^{m} d_{ij}^2 \approx 1 ,\quad d_{ij}\approx \alpha_{i j}^{*} \]
\(Q\) 近似化简为 \[Q=\sum_{i=1}^{m} \sum_{j=1}^{r}{\alpha_{i j}^{*}}^4\color{Gray}\quad \tiny ,\frac{1}{r}\approx \sum_{j=1}^rd_{ij}^2 ,\quad d_{ij}\approx \alpha_{i j}^{*} \]
构造
\[E=\sum_{i=1}^{m} \sum_{j=1}^{r}{\alpha_{i j}^{*}}^4 - \frac{\gamma }{m}\sum_{j=1}^{r}{\left(\sum_{i=1}^{m} d_{ij}\right)}^{2}\]
其中 \(\gamma\) 取 \(\frac{m}{2}\)
因子得分
利用已知的观测值 \(\boldsymbol{X}\) 与构造的因子载荷矩阵 \(\boldsymbol{\Lambda}\) 可以对公共因子测度,即给出公共因子的值。
因子分析的数学模型已经给出,为
\[\left[\begin{array}{c} X_{1} \\ X_{2} \\ \vdots \\ X_{m} \end{array}\right]=\left[\begin{array}{c} \mu_{1} \\ \mu_{2} \\ \vdots \\ \mu_{m} \end{array}\right]+\left[\begin{array}{cccc} \alpha_{11} & \alpha_{12} & \cdots & \alpha_{1 r} \\ \alpha_{21} & \alpha_{22} & \cdots & \alpha_{2 r} \\ \vdots & \vdots & & \vdots \\ \alpha_{m 1} & \alpha_{m 2} & \cdots & \alpha_{m r} \end{array}\right]\left[\begin{array}{c} F_{1} \\ F_{2} \\ \vdots \\ F_{r} \end{array}\right]+\left[\begin{array}{c} \varepsilon_{1} \\ \varepsilon_{2} \\ \vdots\\ \varepsilon_{m} \end{array}\right]\]
注:此处的 \(X_1,X_2\dots;F_1,F_2\dots;\varepsilon_1,\varepsilon_2\dots\) 都表示为一个指标下的一组 \(n\) 个样本的值,即 \(X_i=[x_{i1},x_{i2},\dotsb,x_{in}]\)
原变量 \(\boldsymbol{X}\) 被表示为公共因子的线性组合,载荷矩阵旋转后,公共因子可以做出解释,现在目的是把公共因子用原变量线性表示出来。
记因子得分函数为
\[F_j=c_j+\beta_{j1}X_1+\dotsb+\beta_{jm}X_m,\quad j=1,2,\dots,r\]
要求因子的得分,我们想要得分函数的系数,而因为 \(m>r\) 不能得到精确的得分,载荷矩阵也不存在逆矩阵。
加权最小二乘法(巴特莱特因子得分)
把 \(X_i\) 看作因变量,把因子载荷矩阵看作自变量(不妨设 \(\mu_i=0\) )。
\[\left\{\begin{array}{l} X_{1}=\alpha _{11} F_{1}+\alpha_{12} F_{2}+\cdots+\alpha_{1 r} F_{r}+\varepsilon_{1} \\ X_{2}=\alpha_{21} F_{1}+\alpha_{22} F_{2}+\cdots+\alpha_{2 r} F_{r}+\varepsilon_{2} \\ \cdots \\ X_{m}=\alpha_{\tiny m 1} F_{1}+\alpha_{\tiny m 2} F_{2}+\cdots+\alpha_{\tiny m r} F_{r}+\varepsilon_{p} \end{array}\right.\]
考虑特殊因子方差相异,用加权的最小二乘法,使
\[\sum_{i=1}^m\frac{1}{\sigma_i^2}\left[(X_i)-(\alpha_{i1}\hat{F_1}+\dotsb+a_{ir}\hat{F_r})\right]^2\]
最小的 \(\hat{F_1},\hat{F_2},\dots,\hat{F_r}\) 是相应各个样本的因子得分。
矩阵表示: \[\boldsymbol{X}=\boldsymbol{\Lambda}\boldsymbol{F}+\boldsymbol{\varepsilon}\] 要使 \[(\boldsymbol{X}-\bold{\Lambda}\hat{\boldsymbol{F}})^T\boldsymbol{D}^{-1}(\boldsymbol{X}-\bold{\Lambda}\hat{\boldsymbol{F}})\]
即取偏导,令
\[\frac{\partial \phi(\boldsymbol{F})}{\partial \boldsymbol{F}}=2 \boldsymbol{\Lambda}^{T}(\boldsymbol{X}-\boldsymbol{\Lambda} \boldsymbol{F})=0\]
达到最小,计算得
\[\hat{\boldsymbol{F}}=(\boldsymbol{\Lambda}^T\boldsymbol{\Lambda})^{-1}\boldsymbol{\Lambda}^T\boldsymbol{X}\]
\[\hat{\boldsymbol{F}}=(\boldsymbol{\Lambda}^T\boldsymbol{D}^{-1}\boldsymbol{\Lambda})^{-1}\boldsymbol{\Lambda}^T\boldsymbol{D}^{-1}\boldsymbol{X}\]
这种方法得到的因子得分 \(F_i=[f_{i1},\dots,f_{in}]\) 与主成分分析结果 \(Z_i=[z_{i1},\dots,z_{in}]\),仅仅相差一个常数: \(f_{ij}=z_{ij}/\sqrt{\lambda_j}\)
回归法(汤普森因子得分)
设
\[\left[\begin{array}{c} X_{1} \\ X_{2} \\ \vdots \\ X_{m} \end{array}\right]=\left[\begin{array}{cccc} \alpha_{11} & \alpha_{12} & \cdots & \alpha_{1 r} \\ \alpha_{21} & \alpha_{22} & \cdots & \alpha_{2 r} \\ \vdots & \vdots & & \vdots \\ \alpha_{m 1} & \alpha_{m 2} & \cdots & \alpha_{m r} \end{array}\right]\left[\begin{array}{c} F_{1} \\ F_{2} \\ \vdots \\ F_{r} \end{array}\right]+\left[\begin{array}{c} \varepsilon_{1} \\ \varepsilon_{2} \\ \vdots\\ \varepsilon_{m} \end{array}\right] \] 记第 \(j\) 个因子得分函数为
\[F_j=\beta_{j1}X_1+\dotsb+\beta_{jm}X_m,\quad j=1,2,\dots,r\]
因子载荷矩阵的元素表示了样本和因子的相关系数,有
\[\alpha_{ij}=\gamma_{\tiny X_i F_j}=E(X_iF_j)=E[X_i(\beta_{j1}X_1+\dotsb+\beta_{jm}X_m)]=\beta_{j1}\gamma_{i1}+\dotsb+\beta_{jm}\gamma_{im}\]
有
\[\begin{bmatrix} \gamma_{11} & \gamma_{12} & \dotsb & \gamma_{1m}\\ \gamma_{21}&\gamma_{22} & \dotsb & \gamma_{2m}\\ \vdots & \vdots & \ddots & \vdots \\ \gamma_{m1}&\gamma_{m2} & \dotsb & \gamma_{mm} \end{bmatrix} \begin{bmatrix} \beta_{j1}\\ \beta_{j2}\\ \vdots\\ \beta_{jm} \end{bmatrix}= \begin{bmatrix} \alpha_{1j}\\ \alpha_{2j} \\ \vdots\\ \alpha_{mj} \end{bmatrix}\]
其中三个矩阵分布代表原始变量系数相关系数矩阵 \(\boldsymbol{R}\) 、第 \(j\) 个因子得分函数系数、载荷矩阵第 \(j\) 列。
得
\[\begin{bmatrix} \beta_{11} & \beta_{12} & \dotsb & \beta_{1m}\\ \beta_{21}&\beta_{22} & \dotsb & \beta_{2m}\\ \vdots & \vdots & \ddots & \vdots \\ \beta_{m1}&\beta_{m2} & \dotsb & \beta_{rm} \end{bmatrix}^T=\boldsymbol{R}^{-1}\boldsymbol{\Lambda} \]
因此,因子得分估计为
\[\hat{\boldsymbol{F}}=\boldsymbol{\Lambda}^T\boldsymbol{R}^{-1}\boldsymbol{X}\]
\[\hat{\boldsymbol{F}}=\boldsymbol{\Lambda}^T(\boldsymbol{\Lambda}\boldsymbol{\Lambda}^T+\boldsymbol{D})\boldsymbol{X}\]
司守奎给出的结果有误
两种估计方法的比较
\[\begin{array}{l}\hat{\boldsymbol{F}}(1)=(\boldsymbol{\Lambda}^T\boldsymbol{D}^{-1}\boldsymbol{\Lambda})^{-1}\boldsymbol{\Lambda}^T\boldsymbol{D}^{-1}\boldsymbol{X},\\ \hat{\boldsymbol{F}}(2)=\boldsymbol{\Lambda}^T(\boldsymbol{\Lambda}\boldsymbol{\Lambda}^T+\boldsymbol{D})\boldsymbol{X}\end{array}\]
- 两者得分关系
\[\hat{\boldsymbol{F}}(1)=(I_r+(\boldsymbol{\Lambda}^T\boldsymbol{D}^{-1}\boldsymbol{\Lambda})^{-1})\hat{\boldsymbol{F}}(2)\]
\((\boldsymbol{\Lambda}^T\boldsymbol{D}^{-1}\boldsymbol{\Lambda})^{-1}\) 正定性得到 \(\hat{\boldsymbol{F}}(1)\) 不小于 \(\hat{\boldsymbol{F}}(2)\) ; \(\boldsymbol{\Lambda}^T\boldsymbol{D}^{-1}\boldsymbol{\Lambda}\) 近似 \(0\) 时,结果几乎相等。
- 无偏性
\[E(\hat{\boldsymbol{F}}(1)|\boldsymbol{F})=\boldsymbol{F}\\ E(\hat{\boldsymbol{F}}(2)|\boldsymbol{F})=(I_r+(\boldsymbol{\Lambda}^T\boldsymbol{D}^{-1}\boldsymbol{\Lambda})^{-1})\boldsymbol{\Lambda}^T\boldsymbol{D}^{-1}\boldsymbol{\Lambda}\boldsymbol{F}\]
第一种估计无偏,回归估计有偏。
- 均方误差
\[\mathrm{E}\left[(\hat{\boldsymbol{F}}(1)-\boldsymbol{F})(\hat{\boldsymbol{F}}(1)-{ }^{I} \boldsymbol{F})^{\prime} \mid \boldsymbol{F}\right]=\left(\boldsymbol{\Lambda}^{\prime} \boldsymbol{D}^{-1} \boldsymbol{\Lambda}\right)^{-1} \\ \mathrm{E}\left[(\hat{\boldsymbol{F}}(2)-\boldsymbol{F})(\hat{\boldsymbol{F}}(2)-{ }^{I} \boldsymbol{F})^{\prime} \mid \boldsymbol{F}\right]=\left(I_{m}+\boldsymbol{\Lambda}^{\prime} \boldsymbol{D}^{-1} \boldsymbol{\Lambda}\right)^{-1}\]
这表示第二种估计(汤普森因子得分)有较小的平均预报误差.
缺陷
因子分析是十分主观的,在许多出版的资料中,因子分析模型都用少数可命名因子提供了合理解释。实际上,绝大多数因子分析并没有产生如此明确的结果。评价因子分析质量的法则尚未很好量化,因子分析的质量参差不齐。
参考
- 本文章花费大量时间查询比较各版本的过程,最终以司守奎的参数名为主体,调整了部分参数命名以符合笔者习惯。
- 本文章的格式不清晰,多次差错后依然有公式格式,变量名错误的问题,还请见谅。