回归分析
多元线性回归
模型结构
多元线性回归是研究一个应变量依赖多个自变量的变化关系,并用线性关系刻画的模型。如下:
\[\left\{\begin{matrix} y = \beta_0 + \beta_1 x_1 + \cdots + \beta_mx_m + \varepsilon\\ \varepsilon \sim N(0,\sigma ^2) \end{matrix}\right.\]
其中:\(\beta_0,\beta_1,\dotsb,\beta_m\) 为回归系数;\(x_0,x_1,\dotsb,x_m\) 为变量;\(\varepsilon\) 是误差随机项。
对于 \(n\) 组观测,满足 \(y_i=\beta_{0} + \beta_1 x_{i1} + \cdots + \beta_mx_{im} + \varepsilon_i\) ,记
\[\boldsymbol{Y}=\left[\begin{array}{l} y_{1} \\ y_{2} \\ \vdots \\ y_{n} \end{array}\right] \quad, \quad \boldsymbol{X}=\left[\begin{array}{cccc} 1 & x_{11} & \ldots & x_{1m} \\ 1 & x_{21} & \ldots & x_{2m} \\ \vdots & \vdots & & \vdots \\ 1 & x_{n1} & \ldots & x_{nm} \end{array}\right] \quad, \quad \boldsymbol{\beta}=\left[\begin{array}{c} \beta_{0} \\ \beta_{1} \\ \vdots \\ \beta_{k} \end{array}\right] \quad, \quad \boldsymbol{\varepsilon}=\left[\begin{array}{c} \varepsilon_{1} \\ \varepsilon_{2} \\ \vdots \\ \varepsilon_{n} \end{array}\right]\]
这时模型可以写作:
\[\boldsymbol{Y}=\boldsymbol{X} \boldsymbol{\beta}+\boldsymbol{\varepsilon}\]
参数估计
模型中的参数 \(\beta_0,\beta_1,\dotsb,\beta_m\) 用最小二乘法估计,得到估计值 \(\hat{\beta}_{i}\) 。
需要最小化的函数是:
\[SSE = Q\left(\beta_{0}, \beta_{1}, \ldots, \beta_{p}\right)=\sum_{i=1}^{n}(y_i-\hat{y_i})^2=\sum_{i=1}^{n}\left(y_{i}-\beta_{0}-\beta_{1} x_{i 1}-\ldots-\beta_{p} x_{i p}\right)^{2}\]
为此,令 \[\frac{\partial Q}{\partial \beta _j} =0,(j=0,1,\dots ,m)\]
解得(详细过程参考[3]或[1]): \[\boldsymbol{\hat{\beta}}=\left(\boldsymbol{X}^{T} \boldsymbol{X}\right)^{-1} \boldsymbol{X}^{T} \boldsymbol{Y}\]
记 \(\boldsymbol{\hat{Y}}=\boldsymbol{X}\boldsymbol{\hat{\beta}}\) ,\(\boldsymbol{e}=\boldsymbol{Y}-\boldsymbol{\hat{Y}}\) 为残差,而 \(SSE=\sum e_i^2\) 为残差平方和[1]。
显著性检验
方程显著性检验
检验这个回归方程本身是否有效。我们给出下列原假设和备择假设: \[ H_0: \beta_j=0 , j=1,2,\dots,m\\ H_1: \beta_1,\dots,\beta_m 不全为 0\] 当假设 \(H_0\) 成立时,满足: \[F=\frac{SSR/m}{SSE/(n-m-1)} \sim F(m,n-m-1)\]
式中, \(SSR=\sum_{i=1}^{n}\left(\hat{y}_{i}-\bar{y}\right)^{2}\) 是回归平方和; \(SSE=\sum_{i=1}^{n}\left(y_{i}-\hat{y}_{i}\right)^{2}\) 是残差平方和。再给定的 显著性水平 \(\alpha\) 下,对于上 \(\alpha\) 分位数 \(F_{\alpha}(k, n-k-1)\) , 检验的拒绝域为 \(F>F_{\alpha}(k, n-k-1)\) 接受域可以为:\(F_{1-\alpha/2}(k, n-k-1)<F<F_{\alpha/2}(k, n-k-1)\)。
上式,书上是这样写的,但是好像写错了。 (22.2.8)
注:\(H_0\) 仅说明 \(y\) 与 \(x_1,x_2,\dots,x_m\) 的线性关系不明显,可能存在非线性关系(取对数)。
对于预测型回归需要检查拟合优度(\(R^2\));解释型回归更多的关注模型整体显著性以及自变量的统计显著性和经济意义显著性即可。
\[R^2=\frac{SSR}{SST}=\frac{\sum_{i=1}^{n}(\hat{y_i}-\bar{y})^2}{\sum_{i=1}^{n}(y_i-\bar{y})^2}\] \(R\) 称为复相关系数,\(R^2\) 越大,\(y\) 与 \(x_1,x_2,\dots,x_m\) 相关关系越密切,通常 \(R\) 大于 \(0.8\) 才认为相关性成立[1],这是一个看拟合的好不好的一个综合指标。
系数显著性检验
经过上述验证得到 \(H_0\) ,被拒绝,\(\beta_j\) 不全为 \(0\) ,但不排除存在 \(\beta_j\) 为 \(0\) 。所以还要进行以下 \(m+1\) 个检验。 \[H_0^{(j)}:\beta_{j}=0 , j=0,1,\cdots,m\]
根据无偏性和\(cov(\hat \beta)=\sigma^2(X^{T}X)^{-1}\) [2],得到 \(\hat \beta_j \sim N(\beta_j, c_{jj}\sigma^2)\) ,其中 \(c_{jj}\) 表示 \((X^{T}X)^{-1}\) 的对角线元素 \((j,j)\) 。考虑构造t检验 \(\frac{X}{\sqrt{Y/N}}\)。
\[t=\frac{\hat \beta_j}{\sqrt{c_{jj}}\sigma}=\frac{\hat{\beta_j}/\sqrt{c_{jj}}}{\sqrt{SSE/(n-m-1)}} \sim t(n-m-1)\]
在 \(1-\alpha\) 的置信水平下, \(\beta_j\) 的置信区间为[1]: \[[\hat{\beta_j}-t_{\frac{\alpha}{2}}(n-m-1)s\sqrt{c_{jj}},\hat{\beta_j}+t_{\frac{\alpha}{2}}(n-m-1)s\sqrt{c_{jj}}]\] 其中 \(s=\sqrt{\frac{SSE}{n-m-1}}\) ;或者当 \(|t_j|<t_{\frac{\alpha}{2}}(n-m-1)\) 判断接受 \(H_0^{(j)}\) ,否则拒绝。
检验异方差
残差的方差齐(Equal variance),即LINE原则。即残差的大小不随预测值水平的变化而变化,通常在分析残差的时候,可以通过绘制普通残差或者标准化残差与预测值的散点图进行判断。残差的分布随着变量的取值的增大而呈现扩散趋势产生异方差[5]。
异方差是指各个扰动项的方差不相同,那么方差较大的扰动项破坏模型稳定性的程度就较大[4];因变量的变异程度会随着自身数值或者其他变量的变化而变化,从而不满足残差方差齐性的条件[5]。
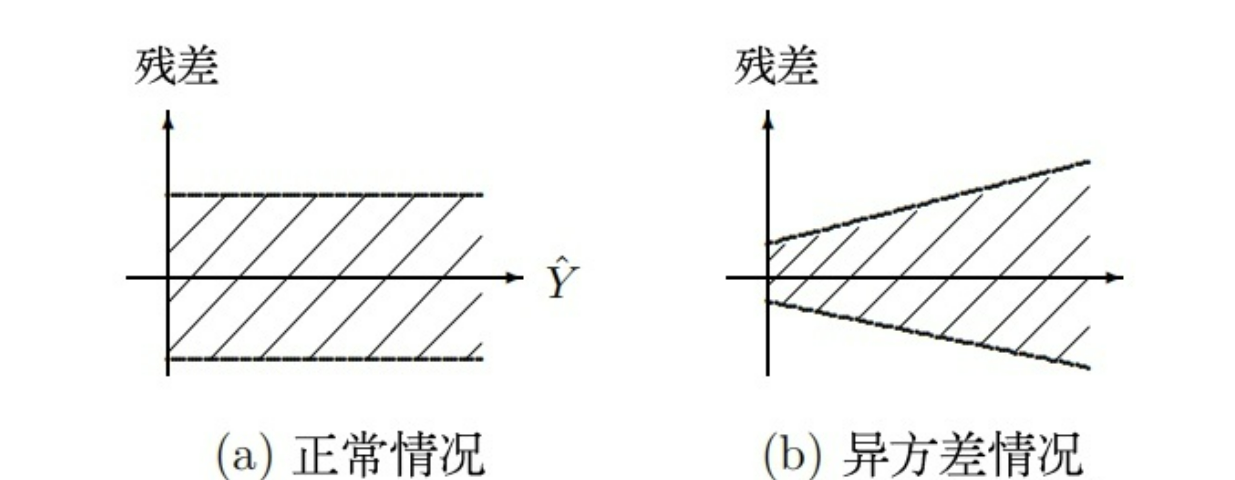
多种检验方法
解决方法
- 构建加权最小二乘法模型
判断导致残差不满足方差齐性的指标,对其加权。
使用“OLS + 稳健标准误”
广义最小二乘法 GLS
检验多重共线性
方差膨胀因子(Variance Inflation Factor)VIF
假设 \(m\) 个自变量中,第 \(j\) 个自变量的 \(VIF=\frac{1}{1-R_{1-m/j}^2}\)
\(R_{1-m/j}^2\) 是将第 \(j\) 个自变量作为因变量,对余下 \(m-1\) 个自变量回归得到的拟合优度,\(VIF_j\) 越大(也就是 \(R_{1-m/j}^2\) 越大),说明当前变量和其他变量关联度越大[4]。记模型:
\[VIF=max(VIF_1,VIF_2,\dots,VIF_m)\]
若,\(VIF > 10\), 则表示回归模型存在严重多重共线性。
注:多重共线性不影响回归方程的解释变量能力与预测能力,只会影响被多重共线性影响的变量的显著性(系数)。解决办法是增大样本或剔除共线性变量。
有时候逐步回归(Lasso回归)是个快捷不动脑子的做法。此外,主成分回归也可用来解决多重共线性的问题。
SPSS实现多元线性回归
岭回归和Lasso回归
岭回归 (Ridge regression)
Lasso(Least absolute shrinkage and selection operator)回归
是一种压缩估计。它通过构造一个惩罚函数得到一个较为精炼的模型,使得它压缩一些回归系数。以损失部分信息、降低精度为代价获得回归系数更为符合实际、更可靠的回归方法,对病态数据的拟合要强于最小二乘法。
\[\left\{ \begin{matrix} 多元线性:\boldsymbol{\hat{\beta }} =argmin_{\hat{\beta }} \sum_{i=1}^{n}(y_i-\boldsymbol{x_i}^T \boldsymbol{\hat{\beta} } )^2 ,其中\boldsymbol{\hat{\beta}}=[\hat{\beta}_1,\hat{\beta}_2,\dots ]\\ 岭回归:\boldsymbol{\hat{\beta } }=argmin_{\hat{\beta }} [ \sum_{i=1}^{n}(y_i-\boldsymbol{x_i}^T \boldsymbol{\hat{\beta}} )^2 + \lambda \sum_{i=1}^n \hat{\beta_i}^2],\lambda>0\\ Lasso回归:\boldsymbol{\hat{\beta }} =argmin_{\hat{\beta }} [ \sum_{i=1}^{n}(y_i-\boldsymbol{x_i}^T \boldsymbol{\hat{\beta} } )^2 + \lambda \sum_{i=1}^n |\hat{\beta_i}|] \end{matrix} \right.\]
其中新增的最后一项\(\sum_{i=1}^n \hat{\beta_i}^2\)称为惩罚函数。
对于岭回归有解为:
\[\boldsymbol{\widehat{\beta}}=\left(\boldsymbol{X}^{T} \boldsymbol{X}+\lambda \boldsymbol{I}\right)^{-1} \boldsymbol{X}^{T} \boldsymbol{y}\]
易知:\(\lambda\) 趋近 \(0\) 时,系数和多元线性回归相同;\(\lambda\) 趋近无穷时,系数趋近 \(0\) 。
Lasso回归相比岭回归,能将不重要的回归系数压缩至 \(0\) ,可以进行降纬,但是没有显式解。
多元二项式回归
Matlab 的统计工具箱提供了多元二项式回归命令 rstool
rstool(X,Y,model,alpha)其中 alpha 为显著性水平(默认为 \(0.05\)), model
有以下四个模型(默认为线性模型)
- \(\operatorname{linear}( 线性 ): y=\beta_{0}+\beta_{1} x_{1}+\cdots+\beta_{m} x_{m}\)
- \(purequadratic (纯二次) : y=\beta_{0}+\beta_{1} x_{1}+\cdots+\beta_{m} x_{m}+\sum\limits_{\tiny j=1}^{\tiny m} \beta_{j j} x_{j}^{2}\)
- \(interaction(交叉) : y=\beta_{0}+\beta_{1} x_{1}+\cdots+\beta_{m} x_{m}+\sum\limits_{\tiny1 \leqslant j<k \leqslant m} \beta_{j k} x_{j} x_{k}\)
- \(quadratic(完全二次) : y=\beta_{0}+\beta_{1} x_{1}+\cdots+\beta_{m} x_{m}+\sum\limits_{\tiny 1 \leqslant j \leqslant k \leqslant m} \beta_{j k} x_{j} x_{k}\)
非线性回归
这里的“线性”是相对于模型参数 \(\beta_0,\beta_1,\dotsb,\beta_m\) 而言的。
对于此类问题,应先给出 \(y\) 与 \(x_1,x_2,\dots,x_n\) 关于 \(\beta_0,\beta_1,\dotsb,\beta_m\) 的非线性表达式。
再使用 Matlab 的 nlpredci 计算回归系数。