插值算法

请注意，本文最后更新于2022.2.6，其中一些理解可能已被笔者证伪或废弃。

定义：给定一组离散点列，要求一条曲线将点依次连接，称之为插值^[1]。

利用已知的点建立合适的插值函数 $f(x)$ ,未知点 $x_i$ 由插值函数 $f(x)$ 可以求得 $(x_i,f(x_i))$ 近似代替未知点^[3]。

作用：利用插值曲线可以对数据进行填充——用少量模拟产生一些靠谱的新数据。

分段插值

分段线性插值

这是最简单也最基础的插值方法，折现统计图的连接方式就是用的分段线性插值。使用函数表时一般直接用该方法。

分段二次插值

取结点 $x_i$ 以及其左右的三个节点 $x_{i-1},x_{i},x_{i+1}$ 进行在区间 $[x_{i-1},x_{i+1}]$ 的二次函数插值，即

$f(x) \approx L_{2}(x)=\sum_{k=i-1}^{i+1}\left[y_{k} \prod_{j=i-1 \atop j \neq k}^{i+1} \frac{\left(x-x_{j}\right)}{\left(x_{k}-x_{i}\right)}\right]$

其意义是用分段抛物线代替 $y=f(x)$ ^[2]。这个方法能保证函数的连续型与一定看起来的平滑性，但是不保证函数光滑，即不保证函数可导。

分段二维插值可以很好的避免多项式插值带来的龙格效应，同时简单易于理解又能看起来平滑，是很常用的方法。

多项式插值

多项式插值的本质是对于 $n+1$ 个互不相同的节点 $(x_i,y_i) (i=0,1,2,\dots,n)$ 求得一个唯一的多项式：

$L_{n}(x)=a_{0}+a_{1} x+a_{2} x^{2}+\ldots+a_{n} x^{n}$

使得 $L_n(x_i)=y_i$ ,即

$\left[\begin{array}{cccc} 1 & x_{0} & \cdots & x_{0}^{n} \\ 1 & x_{1} & \cdots & x_{1}^{n} \\ \vdots & \vdots & \cdots & \vdots \\ 1 & x_{n} & \cdots & x_{n}^{n} \end{array}\right] \left[\begin{array}{c} a_{0} \\ a_{1} \\ \vdots \\ a_{n} \end{array}\right] =\left[\begin{array}{c} y_{0} \\ y_{1} \\ \vdots \\ y_{n} \end{array}\right]$

对于上述范德蒙行列式，易得，$[a_1,a_2,\dotsb]$ 有且仅有一组解。

拉格朗日插值法

上多项式组易解得

$L(x)=y_1\frac{(x-x_2)(x-x_3)...(x-x_n)}{(x_1-x_2)(x_1-x_3)...(x_1-x_n)}+y_2\frac{(x-x_1)(x-x_3)...(x-x_n)}{(x_2-x_1)(x_2-x_3)...(x_2-x_n)}...+y_{n}\frac{(x-x_1)(x-x_2)...(x-x_{n-1})}{(x_{n}-x_1)(x_{n}-x_2)...(x_{n}-x_{n-1})}$

即

$L(x)=\sum_{i=1}^{n}y_i \prod_{j=1,j \neq i}^n \frac{x-x_j}{x_i-x_j}$

为拉格朗日插值法。

注：拉格朗日插值公式在理论分析理解上很容易理解，但是若插值节点发生改变时，插值公式随之就要重新计算生成，在实际计算中会占用大量的计算量。牛顿法的出现正是克服这个问题^[3]。

牛顿插值法

$\begin{aligned} f(x)=& f\left(x_{0}\right)+f\left[x_{0}, x_{1}\right]\left(x-x_{0}\right) \\ &+f\left[x_{0}, x_{1}, x_{2}\right]\left(x-x_{0}\right)\left(x-x_{1}\right)+\cdots \\ &+f\left[x_{0}, x_{1}, \cdots, x_{n-2}, x_{n-1}\right]\left(x-x_{0}\right)\left(x-x_{1}\right) \cdots\left(x-x_{n-3}\right)\left(x-x_{n-2}\right) \\ &+f\left[x_{0}, x_{1}, \cdots, x_{n-1}, x_{n}\right]\left(x-x_{0}\right)\left(x-x_{1}\right) \cdots\left(x-x_{n-2}\right)\left(x-x_{n-1}\right) \end{aligned}$

商差

• 一阶差商

$f\left[x_{i}, x_{j}\right]=\frac{f\left(x_{i}\right)-f\left(x_{j}\right)}{x_{i}-x_{j}} \quad\left(i \neq j, x_{i} \neq x_{j}\right)$

• 二阶差商

$f\left[x_{i}, x_{j}, x_{k}\right]=\frac{f\left[x_{i}, x_{j}\right]-f\left[x_{j}, x_{k}\right]}{x_{i}-x_{k}} \quad(i \neq k)$

• n阶差商

$f\left[x_{0}, x_{1}, \Lambda x_{n}\right]=\frac{f\left[x_{0}, x_{1}, \Lambda, x_{n-1}\right]-f\left[x_{1}, x_{2}, \Lambda x_{n}\right]}{x_{0}-x_{n}}$

由以上定义我们的到差商表如下：

$\begin{array}{cccrcc} x_{i} & y_{i} & \text { 一阶差商 } & \text { 二阶差商 } & \cdots \cdots & n \text { 阶差商 } \\ & & & & \\ x_{0} & f\left(x_{0}\right) & & & \\ x_{1} & f\left(x_{1}\right) & f\left[x_{0}, x_{1}\right] & & \\ x_{2} & f\left(x_{2}\right) & f\left[x_{1}, x_{2}\right] & f\left[x_{0}, x_{1}, x_{2}\right] & \\ & \cdots \cdots & \cdots \cdots & \cdots \cdots & \\ x_{n-1} & f\left(x_{n-1}\right) & \cdots \cdots & \cdots \cdots \\ x_{n} & f\left(x_{n}\right) & f\left[x_{n-1}, x_{n}\right] & f\left[x_{n-2}, x_{n-1}, x_{n}\right] &\dots &f\left[x_{n} \ldots, x_{n}\right] \\ \end{array}$

我们可以得到下面公式：

$\begin{array}{l} f(x)=f\left(x_{\theta}\right)+f\left[x, x_{\theta}\right]\left(x-x_{\theta}\right),\\ f\left[x, x_{0}\right]=f\left[x_{0}, x_{1}\right]+f\left[x, x_{0}, x_{1}\right]\left(x-x_{1}\right),\\ f\left[x, x_{0}, x_{1}\right]=f\left[x_{0}, x_{1}, x_{2}\right]+f\left[x, x_{0}, x_{1}, x_{2}\right]\left(x-x_{2}\right),\\ \cdots \\ f\left[x, x_{\theta}, \cdots, x_{m-1}\right]=f\left[x_{\theta}, x_{1}, \cdots, x_{n}\right]+J\left[x, x_{\theta}, \cdots, x_{n}\right]\left(x-x_{n}\right) \end{array}$

可得到牛顿插值法。

拉格朗日插值与牛顿插值

牛顿插值法和拉格朗日插值法两者都是多项式插值法，本质上，两者的结果相同，只不过表示的形式不同。牛顿插
值法的计算过程具有继承性有易于变动的特点。

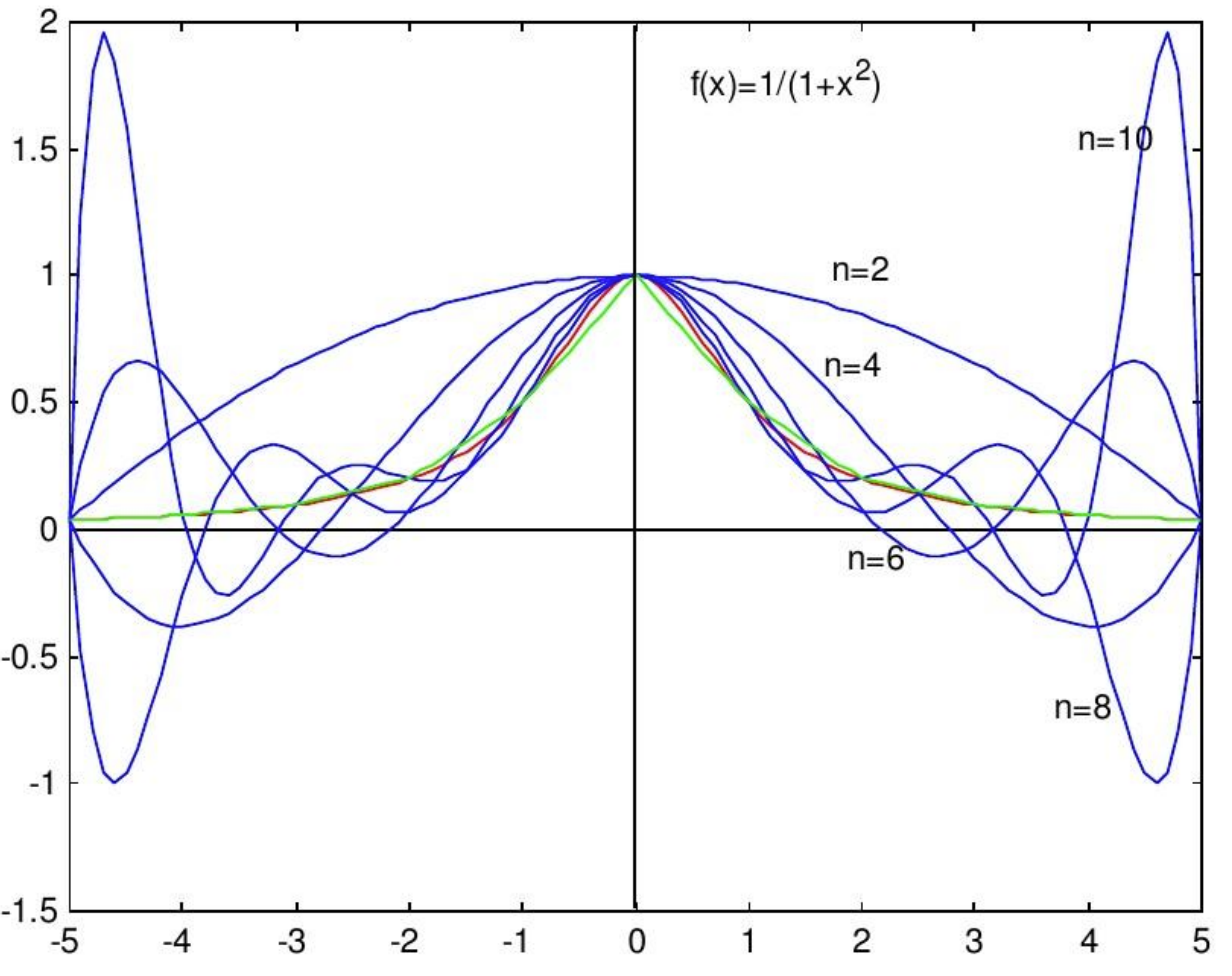
龙格现象

当次数渐高，很容易在多项式插值的边界处产生巨大波动，称为龙格现象。

这里是龙格现象产生原因

埃尔米特(Hermite)插值

不但要求在节点处上的函数值相等，而且还要求对应的导数值也相等，甚至要求高阶导数也相等，满足这种要求的插值多项式就是“Hermite插值多项式”^[4]。

直接使用Hermite插值得到的多项式次数较高，也存在着“龙格现象（Runge phenomenon）”。因此，在实际应用中，往往使用分段三次Hermite插值多项式（PCHIP），来提高“模拟数据的准确性”^[4]。

原理

假定已知函数 $f(x)$ 在揷值区间 $[p, q]$ 上的 $n+1$ 个互不相同的节点 $x_{i}(i=0,1, \ldots, n)$ 处满足 $f\left(x_{i}\right)=f_{i}$ 及 $f^{\prime}\left(x_{i}\right)=f_{i}^{\prime}(i=0,1,2, \ldots, n)$ , 如果函数 $G(x)$ 的存在满足下列条件:

1. $G(x)$ 在每个小区间上的多项式次数为 3 ;
2. $G(x) \in C^{1}[a, b]$ ;
3. $G\left(x_{i}\right)=f\left(x_{i}\right), \quad G^{\prime}\left(x_{i}\right)=f^{\prime}\left(x_{i}\right), \quad i=(0,1, \ldots, n)$
   就称 $G(x)$ 是 $f(x)$ 在 $n+1$ 个节点 $x_{i}$ 上的分段三次埃尔米特插值多项式。

$\begin{aligned} G(x)=& h_{k} y_{k}(x)+h_{k+1} y_{k+1}(x)+H_{k}(x) y_{k}^{\prime}+H_{k+1}(x) y_{k+1}^{\prime} \\ =&\left(1+2 \frac{x-x_{k}}{x_{k+1}-x_{k}}\right)\left(\frac{x-x_{k+1}}{x_{k}-x_{k+1}}\right)^{2} y_{k}+\left(1+2 \frac{x-x_{k+1}}{x_{k}-x_{k+1}}\right)\left(\frac{x-x_{k}}{x_{k+1}-x_{k}}\right)^{2} y_{k+1} \\ &+\left(x-x_{k}\right)\left(\frac{x-x_{k+1}}{x_{k}-x_{k+1}}\right)^{2} y_{k}^{\prime}+\left(x-x_{k+1}\right)\left(\frac{x-x_{k}}{x_{k+1}-x_{k}}\right)^{2} y_{k+1}^{\prime} \end{aligned}$

推广

Hermite 揷值多项式为:

$H(x)=\sum_{i=0}^{n} h_{i}\left[\left(x_{i}-x\right)\left(2 a_{i} y_{i}-y_{i}^{\prime}\right)+y_{i}\right]$

其中:

$h_{i}=\prod_{j=0 \atop j \neq i}^{n}\left(\frac{x-x_{j}}{x_{i}-x_{j}}\right)^{2}, \quad a_{i}=\sum_{j=0 \atop j \neq i}^{n} \frac{1}{x_{i}-x_{j}}$

代码

手写函数

设n个节点的数据以数组 x0（已知点的横坐标），y0（函数值），y1（导数值）输入（注意 Matlat 的数组下标从 $1$ 开始），$m$ 个插值点以数组 x 输入，输出数组 y 为 $m$ 个插值。编

function y=hermite(x0,y0,y1,x);
n=length(x0);m=length(x);
for k=1:m
    yy=0.0;
    for i=1:n
        h=1.0;
        a=0.0;
        for j=1:n
            if j~=i
                h=h*((x(k)-x0(j))/(x0(i)-x0(j)))^2;
                a=1/(x0(i)-x0(j))+a;
            end
        end
        yy=yy+h*((x0(i)-x(k))*(2*a*y0(i)-y1(i))+y0(i));
    end
    y(k)=yy;
end

调用Matlab封装函数

x = -3:3; 
y = [-1 -1 -1 0 1 1 1]; 
xq1 = -3:.01:3;
p = pchip(x,y,xq1);
s = spline(x,y,xq1);
m = makima(x,y,xq1);
plot(x,y,'o',xq1,p,'-',xq1,s,'-.',xq1,m,'--')
legend('Sample Points','pchip','spline','makima','Location','SouthEast')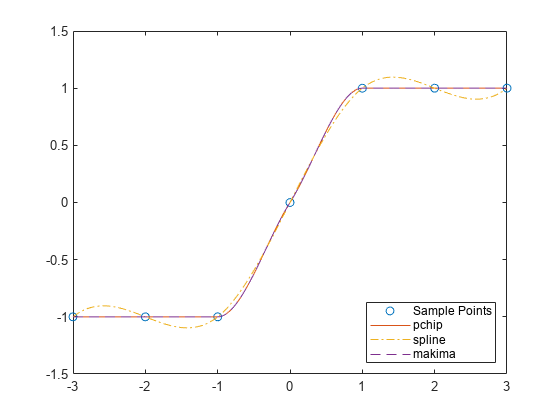

样条插值

所谓样条（Spline）本来是工程设计中使用的一种绘图工具，它是富有弹性的细木条或细金属条。绘图员利用它把一些已知点连接成一条光滑曲线（称为样条曲线），并使连接点处有连续的曲率^[4]。

数学上将具有一定光滑性的分段多项式称为样条函数。

对于 $\Delta : \quad a=x_{0}<x_{1}<\cdots<x_{n-1}<x_{n}=b$ 满足：

1. 在每个小区间 $\left[x_{i}, x_{i-1}\right](i=0,1, \cdots, n-1)$ 上 $s(x)$ 是 $k$ 次多项式。
2. $s(x)$ 在 $[a, b]$ 上具有 $k-1$ 阶连续导数。即 $S_{i}^{(j)}(x_{i+1})=S_{i+1}^{(j)}(x_{i+1})$ $(j=0,1,\dots,k-1)$

一般形式为：

$s_{k}(x)=\sum_{i=0}^{k} \frac{\alpha_{i} x^{i}}{i !}+\sum_{j=1}^{n-1} \frac{\beta_{j}}{k !}\left(x-x_{j}\right)_{+}^{k}$

在实际中最常用的是二次样条函数和三次样条函数。

三次样条生成的曲线更加光滑，相较Hermite更适合曲线(三角函数)。

三次样条插值代码

x = ‐pi:pi;
y = sin(x);
new_x = ‐pi:0.1:pi;
p1 = pchip(x,y,new_x); %分段三次埃尔米特插值
p2 = spline(x,y,new_x); %三次样条插值
pp = csape(x0,y0_ext,conds); %另一个三次样条插值？
plot(x,y,'o',new_x,p1,'r‐',new_x,p2,'b‐')
legend('样本点','三次埃尔米特插值','三次样条插值','Location','SouthEast') %标注显示在东南方向

参考

1. 《数学建模算法与运用》 ↩
2. 清风数学建模 ↩
3. https://zhuanlan.zhihu.com/p/64855561 ↩
4. https://blog.csdn.net/Rayme629/article/details/113174004 ↩
5. https://www.jianshu.com/p/6dfca5f6b249 ↩
6. https://ww2.mathworks.cn/help/matlab/ref/pchip.html ↩